信息学奥赛一本通T1347：格子游戏

【题目描述】

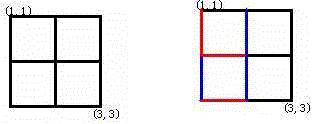
Alice和Bob玩了一个古老的游戏：首先画一个n × n的点阵（下图n = 3）

接着，他们两个轮流在相邻的点之间画上红边和蓝边：

直到围成一个封闭的圈（面积不必为1）为止，“封圈”的那个人就是赢家。因为棋盘实在是太大了(n ≤ 200)，他们的游戏实在是太长了！他们甚至在游戏中都不知道谁赢得了游戏。于是请你写一个程序，帮助他们计算他们是否结束了游戏？

【输入】

输入数据第一行为两个整数n和m。m表示一共画了m条线。以后m行，每行首先有两个数字(x, y)，代表了画线的起点坐标，接着用空格隔开一个字符，假如字符是"D "，则是向下连一条边，如果是"R "就是向右连一条边。输入数据不会有重复的边且保证正确。

【输出】

输出一行：在第几步的时候结束。假如m步之后也没有结束，则输出一行“draw”。

【输入样例】

3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D

【输出样例】

4

【源程序】

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<set>
#include<map>
#include<stack>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 1000001
#define MOD 123
#define E 1e-6
using namespace std;
struct Node{
    int x;
    int y;
}father[210][210],a,b;
Node Find(Node temp)
{
    if(father[temp.x][temp.y].x==temp.x&&father[temp.x][temp.y].y==temp.y)
        return temp;
    return father[temp.x][temp.y]=Find(father[temp.x][temp.y]);
}
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            father[i][j].x=i;
            father[i][j].y=j;
        }

    for(int i=1;i<=m;i++)
    {
        int x,y;
        char ch[10];
        cin>>x>>y>>ch;
        if(ch[0]=='D')
        {
            a=Find(father[x][y]);
            b=Find(father[x+1][y]);
        }
        else if(ch[0]=='R')
        {
            a=Find(father[x][y]);
            b=Find(father[x][y+1]);
        }
        if(a.x==b.x&&a.y==b.y)
        {
            cout<<i<<endl;
            return 0;
        }
        else
            father[b.x][b.y]=a;
    }
    cout<<"draw"<<endl;
    return 0;
}

信息学奥赛一本通T1347：并查集 格子游戏 归属于 并查集，更多同类题解源程序见：并查集 和 格子游戏