信息学奥赛一本通T1277：动态规划经典问题 方格取数
【题目描述】设有N×N的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：某人从图中的左上角A出发，可以向下行走，也可以向右行走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。此人从A点到B点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。【输入】第一行为一个整数N（N≤10），表示N×N的方格图。接下来的每行有三
信息学奥赛一本通T1277：方格取数
【题目描述】
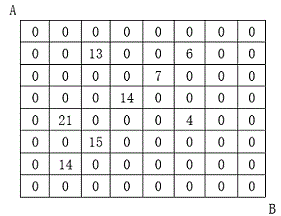
设有N×N的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：
某人从图中的左上角A出发，可以向下行走，也可以向右行走，直到到达右下角的B点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。
此人从A点到B点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。
【输入】
第一行为一个整数N（N≤10），表示N×N的方格图。
接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。一行“0 0 0”表示结束。
【输出】
第一个整数，表示两条路径上取得的最大的和。
【输入样例】
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0【输出样例】
67
【源程序】
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 101
#define MOD 2520
#define E 1e-12
using namespace std;
int g[N][N],f[N][N][N][N];
int main()
{
int n;
int a,b,c;
cin>>n;;
while(scanf("%d%d%d",&a,&b,&c)!=EOF&&a&&b&&c)
g[a][b]=c;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
for(int l=1;l<=n;l++)
{
int temp1=max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]);
int temp2=max(f[i][j-1][k-1][l],f[i][j-1][k][l-1]);
f[i][j][k][l]=max(temp1,temp2)+g[i][j];
if(i!=k&&j!=l)
f[i][j][k][l]+=g[k][l];
}
cout<<f[n][n][n][n]<<endl;
return 0;
}
信息学奥赛一本通T1277：动态规划经典问题 方格取数 归属于 动态规划经典问题，更多同类题解源程序见：动态规划经典问题 和 方格取数
- 发表于 2020-05-04 16:20
- 阅读 ( 759 )
- 分类：信息学奥赛一本通
轩爸
0 篇文章
作家榜 »
-
admin
2 文章
-
张芳
0 文章
-
hanna
0 文章
-
Jason
0 文章
-
lixiaioqian
0 文章
-
GeraldWrora
0 文章
-
董伟
0 文章
-
信奥达人
0 文章
