信息学奥赛一本通T1261：城市交通路网

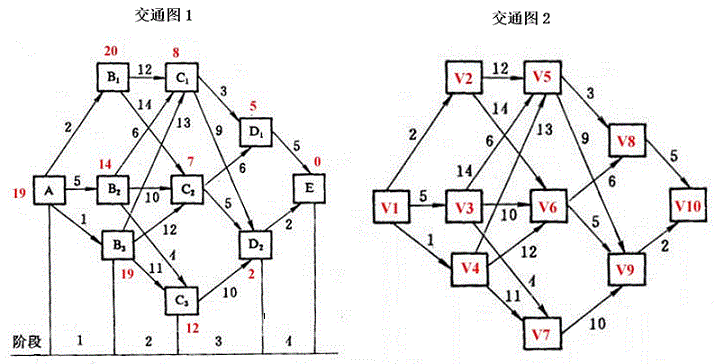
【题目描述】

下图表示城市之间的交通路网，线段上的数字表示费用，单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。

如图：求v1到v10的最短路径长度及最短路径。

【输入】

第一行为城市的数量N;

后面是N*N的表示两个城市间费用组成的矩阵。

【输出】

A->E的最省费用。

【输入样例】

10
0  2  5  1  0  0  0  0  0  0
0  0  0  0 12 14  0  0  0  0
0  0  0  0  6 10  4  0  0  0
0  0  0  0 13 12 11  0  0  0
0  0  0  0  0  0  0  3  9  0
0  0  0  0  0  0  0  6  5  0
0  0  0  0  0  0  0  0 10  0
0  0  0  0  0  0  0  0  0  5
0  0  0  0  0  0  0  0  0  2
0  0  0  0  0  0  0  0  0  0

【输出样例】

minlong=19
1 3 5 8 10

【源程序】

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#include<bitset>
#define PI acos(-1.0)
#define INF 0x3f3f3f3f
#define LL long long
#define Pair pair<int,int>
LL quickPow(LL a,LL b){ LL res=1; while(b){if(b&1)res*=a; a*=a; b>>=1;} return res; }
LL multMod(LL a,LL b,LL mod){ a%=mod; b%=mod; LL res=0; while(b){if(b&1)res=(res+a)%mod; a=(a<<=1)%mod; b>>=1; } return res%mod;}
LL quickMultPowMod(LL a, LL b,LL mod){ LL res=1,k=a; while(b){if((b&1))res=multMod(res,k,mod)%mod; k=multMod(k,k,mod)%mod; b>>=1;} return res%mod;}
LL quickPowMod(LL a,LL b,LL mod){ LL res=1; while(b){if(b&1)res=(a*res)%mod; a=(a*a)%mod; b>>=1; } return res; }
LL getInv(LL a,LL mod){ return quickPowMod(a,mod-2,mod); }
LL GCD(LL x,LL y){ return !y?x:GCD(y,x%y); }
LL LCM(LL x,LL y){ return x/GCD(x,y)*y; }
const double EPS = 1E-6;
const int MOD = 1000000000+7;
const int N = 1000+5;
const int dx[] = {0,0,-1,1,1,-1,1,1};
const int dy[] = {1,-1,0,0,-1,1,-1,1};
using namespace std;

int n;
int G[N][N];
bool vis[N];
int dis[N];
int pre[N];
int f = 1;
void print(int x) {
    if (x == 0)
        return;
    else {
        print(pre[x]);
        printf("%d ", x + 1);
    }
}

int main() {
    scanf("%d", &n);
    memset(dis, INF, sizeof(dis));
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            scanf("%d", &G[i][j]);
            if (G[i][j] == 0)
                G[i][j] = INF;
            else if (i == 0)
                dis[j] = G[i][j];
        }
    }

    dis[0] = 0;
    for (int i = 0; i < n; i++) {
        int minn = INF, x = 0;
        for (int j = 0; j < n; j++) 
            if (!vis[j] && minn > dis[j])
                minn = dis[j], x = j;
        vis[x] = 1;
        for (int j = 0; j < n; j++){
            if (G[x][j] + dis[x] < dis[j]) {
                pre[j] = x;
                dis[j] = G[x][j] + dis[x];
            }
        }
    }
    printf("minlong=%d\n", dis[n - 1]);
    printf("1 ");
    print(n - 1);
    return 0;
}

信息学奥赛一本通T1261：动态规划的基本模型 城市交通路网 归属于 动态规划的基本模型，更多同类题解源程序见：动态规划的基本模型 和 城市交通路网