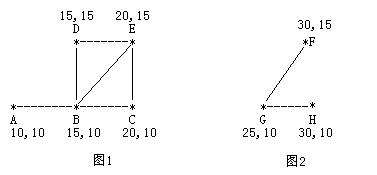信息学奥赛一本通T1343：牛的旅行

【题目描述】

农民John的农场里有很多牧区。有的路径连接一些特定的牧区。一片所有连通的牧区称为一个牧场。但是就目前而言，你能看到至少有两个牧区不连通。现在，John想在农场里添加一条路径 ( 注意，恰好一条 )。对这条路径有这样的限制：一个牧场的直径就是牧场中最远的两个牧区的距离 ( 本题中所提到的所有距离指的都是最短的距离 )。

考虑如下的两个牧场，图１是有5个牧区的牧场，牧区用“*”表示，路径用直线表示。每一个牧区都有自己的坐标：

图１所示的牧场的直径大约是12.07106, 最远的两个牧区是A和E，它们之间的最短路径是A-B-E。

这两个牧场都在John的农场上。John将会在两个牧场中各选一个牧区，然后用一条路径连起来，使得连通后这个新的更大的牧场有最小的直径。注意，如果两条路径中途相交，我们不认为它们是连通的。只有两条路径在同一个牧区相交，我们才认为它们是连通的。

现在请你编程找出一条连接两个不同牧场的路径，使得连上这条路径后，这个更大的新牧场有最小的直径。

【输入】

第 1 行：一个整数N (1 ≤ N ≤ 150), 表示牧区数；

第 2 到 N+1 行：每行两个整数X，Y ( 0 ≤ X，Y≤ 100000 )， 表示N个牧区的坐标。每个牧区的坐标都是不一样的。

第 N+2 行到第 2*N+1 行：每行包括N个数字 ( 0或1 ) 表示一个对称邻接矩阵。

例如，题目描述中的两个牧场的矩阵描述如下：

 A B C D E F G H 

A 0 1 0 0 0 0 0 0 

B 1 0 1 1 1 0 0 0 

C 0 1 0 0 1 0 0 0 

D 0 1 0 0 1 0 0 0 

E 0 1 1 1 0 0 0 0 

F 0 0 0 0 0 0 1 0 

G 0 0 0 0 0 1 0 1 

H 0 0 0 0 0 0 1 0

输入数据中至少包括两个不连通的牧区。

【输出】

只有一行，包括一个实数，表示所求答案。数字保留六位小数。

【输入样例】

8
10 10
15 10
20 10
15 15
20 15
30 15
25 10
30 10
01000000
10111000
01001000
01001000
01110000
00000010
00000101
00000010

【输出样例】

22.071068

【源程序】

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<string>
#include<cstdlib>
#include<queue>
#include<vector>
#include<set>
#define INF 0x3f3f3f3f
#define PI acos(-1.0)
#define N 1001
#define MOD 123
#define E 1e-6
using namespace std;
int x[N],y[N];
char s[N];
double g[150+10][150+10],f[150+10];
double calculate(int x1,int y1,int x2,int y2)
{
    return sqrt((double)(x1-x2)*(x1-x2)+(double)(y1-y2)*(y1-y2));
}
int main()
{
    int n;
    cin>>n;

    for(int i=1;i<=n;i++)
        cin>>x[i]>>y[i];
    for(int i=1;i<=n;i++)
    {
        scanf("%s",s+1);
        for(int j=1;j<=n;j++)
        {
            if(i!=j)
            {
                if(s[j]=='0')
                {
                    g[i][j]=INF;
                    g[i][j]=INF;
                }
                else
                {
                    g[i][j]=calculate(x[i],y[i],x[j],y[j]);
                    g[j][i]=calculate(x[i],y[i],x[j],y[j]);
                }
            }
            else
                g[i][j]=0;
        }
    }

    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                if(g[i][j]>g[i][k]+g[k][j])
                    g[i][j]=g[i][k]+g[k][j];

    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if(g[i][j]<INF&&g[i][j]>f[i])
                f[i]=g[i][j];

    double minn=INF;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            if( g[i][j]==INF && minn>f[i]+f[j]+calculate(x[i],y[i],x[j],y[j]) )
                minn=f[i]+f[j]+calculate(x[i],y[i],x[j],y[j]);

    for(int i=1;i<=n;i++)
        if(minn<f[i])
            minn=f[i];

    printf("%.6lf\n",minn);
    return 0;
}

信息学奥赛一本通T1343：最短路径算法 牛的旅行 归属于 最短路径算法，更多同类题解源程序见：最短路径算法 和 牛的旅行